Physics

Introduction to Kinematics

Kinematics is the branch of mechanics that describes the motion of objects without considering the forces that cause the motion.

Key Concepts

Distance

Distance between two points is the length of actual path travelled by the particle. It is a scalar quantity. Unit : m(metre).

Displacement Example

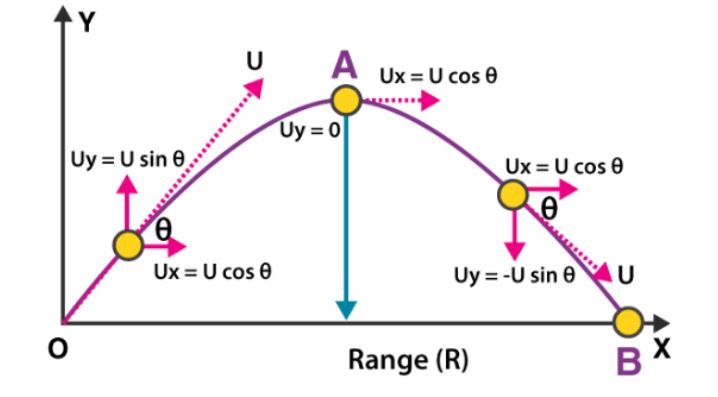
Displacement

Displacement is a vector drawn from the initial position (A) to the final position (B) Unit : m(metre)

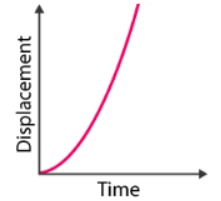
Displacement Example

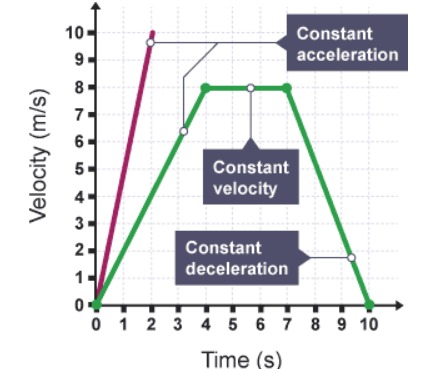
Velocity

Velocity is the rate of change of position vector. Kinematics Unit : ms–1 (metre per second)

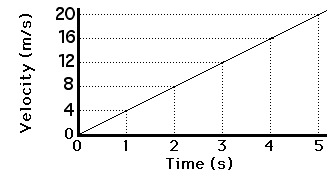
Velocity Example

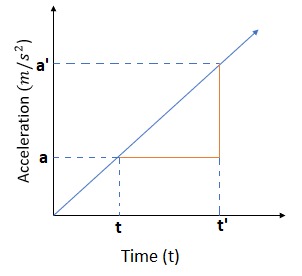
Acceleration

Acceleration is defined as the rate of change of velocity. It is denoted by ‘a’ and is measured in the units of m/s2

Acceleration Visual

Average speed vs Average velocity

Avg speed

The average speed of an object can be defined as the total distance travelled by it in a particular interval of time. It can be calculated by dividing the total distance travelled by the total time taken. average speed (avg) = Total distance covered/ Total time taken

Avg velocity

Average velocity is a vector quantity. Average velocity is defined as the change in position or displacement (∆x) divided by the time intervals (∆t) in which the displacement occurs.The average velocity can be positive or negative depending upon the sign of the displacement. The SI unit of average velocity is meters per second (m/s or ms-1)

Characteristics of v-t graph

The velocity of an object is its speed in a particular direction. Two cars travelling at the same speed but in opposite directions have different velocities. A velocity-time graph shows the speed and direction an object travels over a specific period of time. Velocity-time graphs are also called speed-time graphs. When an object is moving with a constant velocity, the line on the graph is horizontal. When the horizontal line is at zero velocity, the object is at rest. When an object is undergoing constant acceleration, the line on the graph is straight but sloped. Curved lines on velocity-time graphs also show changes in velocity, but not with a constant acceleration or deceleration. The diagram shows some typical lines on a velocity-time graph.

graphical representation of motion

Slope of tangent to position time graph gives velocity. Slope of tangent to v−t curve gives acceleration. Area enclosed between v−t curve and time axis between an interval of time gives displacement. Slope of tangent to a−t curve gives rate of change of acceleration Area enclosed between a−t curve and time axis between an interval of time gives change in velocity

v-t graph

Equations of Motion

For constant acceleration, the following equations are used:

1st Equation

v = u + at

2nd Equation

s = ut + ½at²

3rd Equation

v² = u² + 2as

Projectile motion

When a particle is thrown obliquely near the earth’s surface, it moves along a curved path under constant acceleration that is directed towards the centre of the earth (we assume that the particle remains close to the surface of the earth). The path of such a particle is called a projectile and the motion is called projectile motion

v-t graph

Total Time of Flight: Resultant displacement (s) = 0 in Vertical direction. Therefore, by using the Equation of motion: gt2 = 2(uyt – sy) [Here,uy = u sin θ and sy = 0] i.e. gt2 = 2t × u sin θ
1. Along the x-axis: uniform velocity, responsible for the horizontal (forward) motion of the particle. 2. Along y-axis: uniform acceleration, responsible for the vertical (downwards) motion of the particle

Example Questions

1. Bird is flying in north-east direction with or v = 4√2 m/s with respect to the wind and the wind blowing from north to south with speed 1 m/s. Find the magnitude of the displacement of the bird in 3 sec?

Solution:

2. A stone is thrown vertically upward with a velocity of 20 m/s. How long does it take to return to the thrower's hand?

Solution: Total time = 2u/g = 40/9.8 ≈ 4.08 s

3. A car is moving with velocity 72 km/h. If brakes are applied to stop the car in 10 s, find acceleration and distance.

Solution: v = 0, u = 20 m/s, t = 10s ⇒ a = -2 m/s², s = ut + ½at² = 200 - 100 = 100 m

4. A person throws a stone vertically upwards with velocity u. If it reaches max height in 5 s, find u.

Solution: At max height, v = 0 ⇒ v = u - gt ⇒ 0 = u - 10×5 ⇒ u = 50 m/s

5. A train moves with uniform acceleration from rest. It attains 40 m/s in 20 s. Find distance traveled.

Solution: u = 0, v = 40, t = 20 ⇒ s = ut + ½at² = 0 + ½ × 2 × 400 = 400 m